Warning: Programmer art ahead. Does not reflect the artistic quality of this studio. At all.
Here at PolyKnight Games, we’re making InnerSpace, which takes place in inverted planetoids. This is really cool, but it brings up a lot of technical issues. There are things we can’t do the typical way. We share plenty of technical issues that are faced by games that use regular planetoids, but with some added “fun” on the development side. That being said, I’ll cover the core of the issue.
We face two base issues:
- Which ways are up, north, and east?
- What are my current coordinates?
The first thing to define is up, north, and east, based on your location in the sphere. In defining this we need to create arrows that point in the direction you must travel to reach the center of the sphere (up), to reach the north pole (north), and to reach what we’ll call the east-pole (east). The east-pole is the eastern most point of the planet, just like the north-pole is the northern most point. This then defines a “local” coordinate system, which tells us which way is up, north, and south, see the picture below.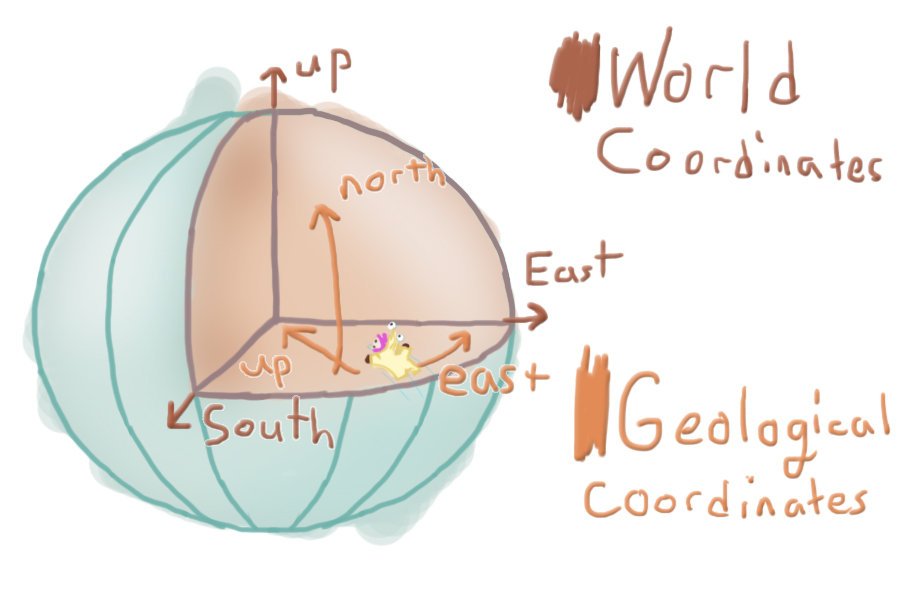
Next up we want to utilize a different coordinate system, which describes the player’s location inside the sphere. The traditional coordinate system is called Cartesian coordinates and is organized in 3d-space with three values: (x, y, z). This is a fine coordinate system, as the y value normally describes your distance from the ground and the x and z coordinates describe your location in space, but this isn’t fitting for a sphere. Y does not define distance from the ground anymore and x nor z describe distance traveled. Geographical coordinates are defined by angle from the equator and angle traversed around the equator. It utilizes longitude and latitude, which replace x and z for distance traveled, and height, which replaces y for distance off the ground. Calculating this isn’t as useful in a technical sense, although it’s very useful to the player. This coordinate makes traversing the planet: #1 feel very official, and #2 Is more organized. It’s easier to read and is less information than (x, y, z) coordinates. The height, however, is useful. We exclusively use this calculation for plotting maps, as the player takes the role of a cartographer.
If you’re interested in this from a programming perspective, you’ll want to make sure you’re fresh on your vector operations and your trigonometry. I use a lot of Unity’s operations for example sake, but you’ll likely want to write out these equations yourself (I won’t explain the difference between vector operations / calling Vector3.Angle(a, b) and using a Asin(theta)/Dot product with proper vector projections (which accounts for planetary rotation)).
What this affects
- Direction of gravity (which way is down/up?)
- Used to orient AI, so birds don’t fly upside down
- Physics objects, so they don’t fly sideways
- Curve fitting/modeling, so the plane dives to the closest water
- Height into atmosphere or distance from water surface
- Height based effects, so the water russles
- Physics object gravity strength, if we want gravity to get stronger
- AI pathfinding, so something can fly along the water’s surface
- Player map & coordinates, so we we know where we are at and can mark key locations logically
- Pretty much everything
Orientation
We will solve based on object location relevant to the current planet. As you can see in the image above, green denotes up, blue defines north, and red defines east. The thinner lines attached to each of the spheres denote the recalculated directionality.
The east and north are calculated as tangents of the arc, meaning they are representative of the sphere’s curvature at that exact point as a straight line. They do not point to the pole, but instead the direction you would need to travel to reach the north or eastern poles, while maintaining your current height.
Here’s some pseudo-code:
- Define up based on relative position to planet.
- objectUp = (objectPosition – planetPosition) * -1
- Use cross products to derive east and north
- objectEast= Cross(worldUp, objectUp)
- objectNorth = Cross(objectUp, objectEast)
Unity’s vector cookbook in-case you’re rusty on vector operations.
Coordinates
For coordinates, we will convert our typical Cartesian coordinates (x, y, z) to geographic coordinates (longitude, latitude, and height). For usual geographical coordinates, height (ht) is defined by distance off the surface (further from center). For InnerSpace we’re backwards: height is defined by distance from the center (closer to the center). Height becomes negative as you go further into the water, or past the surface (further from the center). I calculate longitude and latitude the same as a standard (spherical) planet, though.
Here’s some pseudo-code:
- Project the object’s relative position onto the planet’s xz-plane
- vMod = pos – planetPos
- vMod.y = 0
- Calculate longitude as the angle between the planet’s forward and your projected vector.
- longitude = Angle(vMod, planet.forward)
- if (relPos.x < 0) longitude *= -1
- turns the value negative if it’s on the dark-side of the planet
- Calculate latitude as the angle between the projected vector and the actual relative vector.
- latitude = Angle(vMod, relPos)
- if (relPos.y < 0) latitude*= -1f
- turns the value negative if it’s on the dark-side of the planet
- Calculate the height based on the relative position of the object and the planet’s radius. Invert the value.
- height = (relPos – planetRadius) * -1
My source code (in C# for Unity3D)
Movement animation in the .gif isn’t included. I implemented this differently for the game (mostly structurally and slight modifications to the what I calculate it). But this serves as the simplest and shortest example I could think of. I didn’t comment the code, as I think the code is pretty self explanatory. If you have any questions, drop a comment down below!
Summary
The fix to this problem is simple: redefining up, east, and north requires little code. It’s far reaching, and if you make a game like this, you’ll find yourself using these ideas, often. Write the code in a way that’s easily accessible (I’m currently using a static class that belongs to an easy to type namespace). Another method could be to extend the MonoBehavior object, but that makes it inaccessible from objects that don’t extend it. And to the non-programmers that are terribly confused, I’m sorry that you couldn’t make up-or-down of this topic (pfufu).
Next time…
Collisions. How can you be inside a sphere, but not hit the edge? How do we handle detection that you are inside the sphere, dry, or outside of the sphere, wet?

This was a great write up! Awesome implementation on a different gravity/coordinate style. I am excited to actually see this game when the kickstarter goes up.
Thanks mate! It’s simple, but that’s the goal!
Line 58 ( vMod.y = 0f; ) looks like you’re assuming the planet’s axis is always completely aligned with the game’s world Y axis. If I wanted planets with tilted axis’, would I create vMod by projecting the RelPos vector onto the planet’s XZ plane?
As for the MonoBehaviour inheritance issue, maybe using extension methods to Transform would be good? For example:
public static Directionality GetDirectionality(this Transform transform)
{
Directionality direction = new Directionality();
direction.up = relPos.normalized * -1f;
direction.east = Vector3.Cross(Vector3.up, direction.up).normalized;
direction.north = Vector3.Cross(direction.up, direction.east).normalized;
return direction;
}
The issue with the extension method above however, is that relPos is undefined, and requires some sort of workaround since relPos is a property. Although, since relPos traces back to where you would store the object’s related planet transform, maybe this exposes a need for an appropriate data structure for mapping objects to planets.
I suppose you could just pass the planet’s transform as a parameter and solve half the problem.
public static Directionality GetDirectionality(this Transform transform, Transform planet)
{
Directionality direction = new Directionality();
Vector3 relPos = transform.position – planet.position;
direction.up = relPos.normalized * -1f;
direction.east = Vector3.Cross(Vector3.up, direction.up).normalized;
direction.north = Vector3.Cross(direction.up, direction.east).normalized;
return direction;
}
I think this would at least lead to a useful set of math utility methods.
Ah, I had a line about the .y=0 thing, but I must have deleted it when I was editing this article. I’ll add in a comment to the source for this, although I did mention the abstract goal of that line the crappy-pseudo “Project the object’s relative position onto the planet’s xz-plane.”
In my personal source, which is just a static class of math methods I call (after “using” the namespace), I use a more complicated method. You can project onto the object’s XZ plane, although I find it easier to transform into the object’s local space using it’s world to local matrix. This accounts for the “relative position” calculation and also accounts for the rotation, which also lets you use the simpler and easier reading calculations in some of the methods. This all said, I have this same object written a good three times and I’m yet to run stress tests or think about it really hard to see which method is actually faster (I’ll have to edit the article when I do). From a readability standpoint, the matrix method is my favorite.
I actually had not heard of Extension methods honestly, I spent an hour screwing around with them as of now. I was looking for this! I had gone as far to modify unity’s editor for the transform itself (graphically), but in the code of other objects that wasn’t useful. That being said, in reality the use isn’t too different. CU.getUniverseCoordinates(transform) vs transform.getUniverseCoordinates(), although the philosophy of how you access it is very very different.
I personally have a class “DryWetEntity” that extends “Entity,” these objects are the only bits of code that actually utilize these methods. Meaning, if I want these coordinates, I actually get the “DryWetEntity” or “Entity” class, which also contains other useful information on the object. Inside “Entity” where I use and store these calculations (I just fetch values elsewhere from the class), which keeps me from recalculating the values across multiple monobehaviors. Another tidbit they contain is code that determines which planet they belong to, since you might switch planets.
Edit: grammar
Ok, thanks for clarifying about the vMod.y = 0. Yea, extensions can be seen as C#’s streamlined way of handling what would be a utility class in Java. As shown in your reply, you have to create some new class to store the data. I’m not sure exactly what your requirements are, so it’s understandable that you might not need extension methods here.
I personally would have these calculations as an extension to transform, but still store the resulting calculation in the entity. Alternative to the entity, a static class managing a table hashed by GUIDs to map a GameObject to cached calculations might be something useful to the project in the long run and a place to store this directionality calculation for example. I feel using the extension methods are a bit more organized (all transform related data and operations in Transform), and you’re not passing the transform as a parameter as often in your code which I would also say is a safer practice. As for the world to local matrix, do you really need to get the matrix? There’s Transform.InverseTransformPoint, which is what I regularly use.
I’m just curious at this point, the example code was well written and easy to understand 😛
Actually planning on mapping gravitational direction on a grid for the “InnerSpace.” So I’ll just do something like pos*0.1 and ceil the values to find object’s index in the grid. I can just calculate it all before hand in editor instead of caching it at run-time. I guess that’s a pretty similar solution though. Regarding application, I just don’t like giving myself options. If I toss it on a transform, I might access it that way without thinking, instead I want it all in the Entity class. It’s just application specific, I think the transform extension is way more elegant though.
Yeah, I keep finding myself using matrices, it’s a habit from writing openGL programs from scratch. I believe the calculation is identical, just a bit more compiler/source work on my end (1 more line). I should switch over.
I was so glad to see this game the other day. I’ve been trying to find out how to do something similar but with the O’Neil cylindrical space station in mind. This was really helpful, good luck with the game
Thanks! I’m glad to be of assistance. Hopefully we’ll be sharing many of our solutions along the game’s development.
It is tough to locate knowledgeable people today on this subject, but you sound like you understand what you’re talking about! Thanks